Practitioner-Lead Action Research project undertaken at Kirklees College
during two academic semesters in 2015 into correlation between teaching and learning both English grammar and mathematics.
The project was carried out with the support of emCETT
Over decades, numerous approaches and methods to teaching and learning languages have been developed and, each time, regarded as the most effective. Recently, in the post-method era, language teaching seems to have been focused on the ability to communicate fluently, even at the expense of accuracy. This reseach project is not an attempt at proving that English language and mathematics are exactly the same but there are some aspects of language which require the same 'precision' as mathematics and can be viewed and taught the same way.
Over 19 years old students of ESOL (English for Speakers of Other Languages) and Adult Numeracy were involved in the project.
- Learning vs acquisition. Learning is seen as a conscious process of studying English as opposed to the subconscious process of ‘picking up’ the language (Crystal, 2003)
- Formal instruction which is understood to refer to grammar teaching (Ellis, 1994)
- Inductive vs deductive way of instruction. Inductive (more traditional) method where the rules are explained and examples are given to practise
Support from other areas:
- Cognitive studies -metacognition - inductive reasoning
Research into analogical reasoning shows that even 3-year-old children succeed in the item analogy task (Goswami & Brown, 1989)
40 students were asked three questions to find out their opinions about their competence concerning English grammar and Maths. The questions were as follows:
The first two questions were given to start students thinking about the two areas and only the last one was used to collate the results regarding their competence.
Over 19 years old students of ESOL (English for Speakers of Other Languages) and Adult Numeracy were involved in the project.
My teaching has been based on the idea of rules governing both English language and mathematics. The rules existent in English and mathematics are understood as tenses and formulae respectively. I believe that they can be instructed the same way. The instruction involved presenting the rules and students completing the tasks.
Two main English tenses were chosen and the instruction including the tasks for students were planned as follows:
Students needed to use the regular verbs with the –ed suffix to create sentences in both tenses.
Regarding mathematics I selected four tasks around the formulae of working out the area and perimeter of shapes and discounts.
The tasks involved working out:
The area of triangles (2) and working out the discount (4) both required students to multiply two numbers and division by another to get the result.
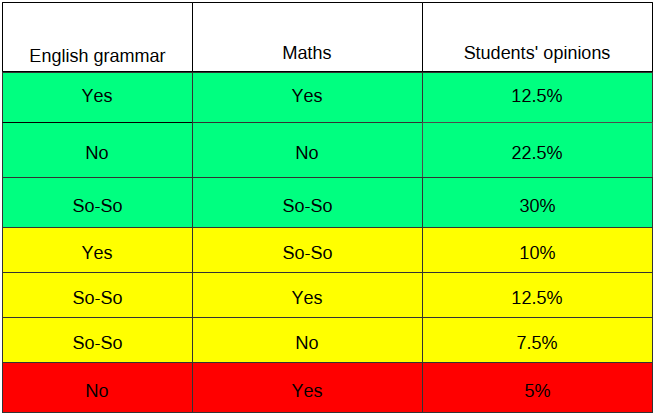
The questionaires were used to assess students' own competence in English grammar and mathematics. The students were given three options to answer which were: yes, no, and so-so. It was, however, the correlation between the answers which we were interested in. The same answers for two areas, irrespective of the opinion, meant that there is a correlation between them. I considered it to be a partial correlation when students assessed one of the areas as ‘so-so’. There was no correlation when students gave to distinct answers e.g. Yes for mathematics and No for English grammar. As a result I got the percentages as follows:
T1. Percentages of students' opinions of the levels of competency in English grammar and maths.
After the instruction students were given a short test to find out if they were able to follow the rule. To be able to compare the results with their opinions I used the percentages to establish the competence using the same criteria as the students’ answers in the questionnaires as yes ( percentage of correct answers between 67% and 100%), no ( percentage between 0% and 33%), and so-so ( percentage between 34% and 66%).
T2. Percentages of students' opinions and test results of the levels of competency in English grammar and maths.
Looking at the results, the considerable discrepancies between the students’ opinions and the results of the test can be seen. The 12.5 % for good competence in both areas has increased up to 84.21% of what students could actually do. A slight decrease in the percentage of the rest of the students’ answers is evident.
Although it is the correct answers that give us information to work with, I also looked at the incorrect answers and we noticed:
- overgeneralization (the extension of grammatical rule beyond it’s normal use (Crystal, 2003) e.g. ‘waterred’ (18% of students applied the rule of doubling the last consonant even though the stress in this word makes it an exception to the rule), ‘listenned’ (23%),’plaied ‘or ‘plaid’ (18% even though it is an irregular verb). There were examples of applying the rules by spelling ‘help’, ‘explain’ and ‘disturb’ as ‘helped’, ‘explained’, ‘disturbed’.
- confusion with the subject- using ‘have’ or ‘has’ with the subjects they normally do not go with e.g. Sarah have, I has, the woman have, we has..
Some of the incorrect answers in mathematics were as follows:
- wrong number for percentage used but the correct calculation done e.g. subtraction
- wrong number for discount taken away e.g. £2 instead of £2.50 but the correct calculation applied e.g. subtraction
- ‘incorrect’ method used as opposed to one shown and explained e.g. multiplication to work out the perimeter instead of given addition to do
All of the above examples of inappropriate answers are still a proof of students applying the rules which they were instructed with.
Comparing the results of students’ opinions and the results of the test following the instruction I have drawn the following conclusions:
- in both areas students are more capable than they think
- students can follow a rule once formally instructed and shown
- to both English and mathematics, generally regarded as distinct areas, one way of instruction can be used to improve certain aspects in both areas.
- there is a correlation between the level of competence in English grammar and mathematics
The analysis of the rest of inappropriate answers as well as discussions with some students while working on the project I have identified the following issues:
- ‘commited’ spelled with one ‘t’ by 44% percent of students and ‘fited’ by 14% can be an indicator of not applying the rule correctly to the words they do not know or students being familiar with the ‘easier’ words and not actually applying the rule
- students relying on spellings they have learnt in a different way but not by applying the rules
- remembering the formulae for the future
To eliminate the above factors a further study is needed over a longer period of time. Although it appears to be a more complex process, there is an indication of the ability to follow rules in both areas even by the students who regard themselves or are regarded as having low competence in English grammar and mathematics.